Рассмотрим такую задачу: дано множество из n чисел; нужно найти тот его элемент, который будет i-м по счёту, если расположить элементы множества в порядке возрастания. Такой элемент называется i-ой порядковой статистикой. Будем нумеровать элементы в стиле языка С. Тогда минимум - это нулевая порядковая статистика, а максимум - это (n-1)-ая порядковая статистика. Медианой называется порядковая статистика номер n/2. Известно, что порядковую статистику можно найти за время O ( n ). Функция selectR делает это в среднем ( в худшем случае за O ( n2 ) ), а функция select7 и в худшем случае: Def<double> select7 ( CArrRef<double> a, nat i ); template <class T> Def<T> selectR ( CArrRef<T> a, nat i ); Функция select7 использует поиск медианы семи чисел, а функция selectR псевдослучайные числа. Сравнительные тесты показали, что selectR обычно работает быстрее, чем select7. Следующая функция select осуществляет частичную сортировку исходного массива: template <class T> bool select ( ArrRef<T> a, nat i );После её применения выполняется условие: если j < i, то a[j] <= a[i], если j > i, то a[j] >= a[i]. Сравнительные тесты показали, что select работает быстрее, чем selectR. Каждому числу можно сопоставить вес ( неотрицательное число ), тогда порядок будет определять число p, значение которого находится в интервале от 0 до 1. 0 - соответствует минимуму, 1 - максимуму, 1/2 - медиане, а вообще нужно найти число такое, чтобы сумма весов чисел меньших его делённая на общий вес была меньше или равна p, а сумма весов чисел больших его делённая на общий вес была меньше или равна 1 - p. Таким образом определяются взвешенные порядковые статистики. Здесь необязательно, чтобы сумма всех весов была равна 1. Следующая функция находит заданную взвешенную статистику и возвращает результат в виде индекса, что в некоторых случаях удобнее: template <class T1, class T2> Def<nat> selectR ( CCArrRef<T1> & a, CCArrRef<T2> & w, T2 p, ArrRef<nat> & buf );В этой функции члены массива а с нулевым весом игнорируются, а в случае обнаружения отрицательных весов функция завершает работу и возвращает неопределённое значение. Размер вспомогательного массива buf должен быть не меньше, чем удвоенный размер массива а. Следующие две функции вычисляют сглаженные порядковые статистики, т.е. функция от p получается гладкая ( без скачков ). Функция selectS применяет прямоугольную функцию сглаживания, а функция selectT - треугольную: Def<double> selectS ( ArrRef<SortItem<double> > s, double p, double r ); Def<double> selectT ( ArrRef<SortItem<double> > s, double p, double r );Здесь, как и выше, 0 <= p <= 1, а r - радиус окна усреднения. Элементы массива s в поле head содержат порядок, а в поле tail - вес. После вызова этой функции массив s будет упорядочен по возрастанию. На рисунке ниже показаны 3 графика ( функции от р ) - selectR ( красный ), selectS ( синий ) и selectT ( зелёный ): 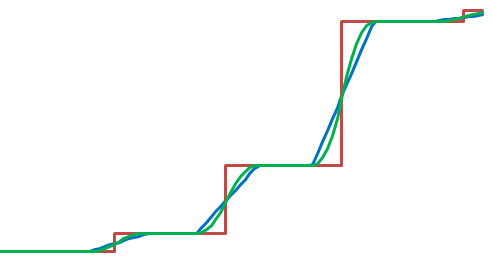 На графике selectR вертикальные отрезки изображены условно ( на самом деле там разрывы горизонтальных отрезков ). Графики selectS и selectT не имеют разрывов, но функция selectS имеет разрывы первой производной, а у функции selectT первая производная непрерывна. Радиус окна усреднения r = 1/16. Описание шаблонов классов CArrRef, ArrRef и CmbArray находятся здесь.
|