Аппроксимация функций

Пусть заданы значения функции в некоторых точках и степень полинома. Необходимо выбрать коэффициенты полинома так, чтобы минимизировать отклонения от заданных значений функции. Обычно минимизируют сумму квадратов отклонений, т.е. решают задачу наименьших квадратов. Известно несколько способов решения этой задачи. Ниже представлены два из них. 

bool apprLSS_H ( nat n, CArrRef<double> x, CArrRef<double> y, nat m, ArrRef<double> c );

bool apprLSS_O ( nat n, CArrRef<double> x, CArrRef<double> y, nat m, ArrRef<double> c );

Первый из них решает задачу наименьших квадратов при помощи преобразований Хаусхолдера. В моих экспериментах этот способ давал наилучшую точность в сложных случаях.
Второй способ использует для решения ортогонализацию Грамма-Шмидта и работает несколько быстрее предыдущего.

Входными данными являются: количество исходных точек, ссылки на массивы x и y, количество коэффициентов полинома и ссылку на них. Обратите внимание, что m - это не степень полинома, а количество коэффициентов. Степень полинома равна m-1.

Для аппроксимации периодических функций предлагаются следующие классы, которые представляют собой разложение Фурье. Конструкторы этих классов имеют два параметра. Первый параметр (func) - это массив значений функции в некоторых точках (xi, yi), второй параметр (nr) - это максимальная гармоника, а третий (k) - коэффициент симметрии. Период функции равен 2*M_PI. 
class HarmAppr
{
protected:
    nat ks;
    DynArray<double> coef;
    HarmAppr () {}
public:
    HarmAppr ( CCArrRef<Vector2d> & func, nat nr, nat k = 1 );

    double operator () ( double a ) const;
};
Класс HarmApprMod предназначен аппроксимация периодических функций с возможностью изменения отдельных значений исходной функции (метод rebuild). 
class HarmApprMod : public HarmAppr
{
    HMatrix<double> mat;
public:
    HarmApprMod ( CCArrRef<Vector2d> & func, nat nr, nat k = 1 );

    void rebuild ( ArrRef<Vector2d> & func, nat iy, double y );
};
Класс HarmAppr2 делает аппроксимацию периодических функций при помощи метода наименьших квадратов: 
class HarmAppr2 : public HarmAppr
{
    nat rank;
public:
    HarmAppr2 ( CCArrRef<Vector2d> & func, CCArrRef<bool> & w, nat nr, nat k = 1 )
    {
        rebuild ( func, w, nr, k );
    }

    bool rebuild ( CCArrRef<Vector2d> & func, CCArrRef<bool> & w, nat nr, nat k );
    bool rebuild ( CCArrRef<Vector2d> & func, CCArrRef<bool> & w, nat nr )
    {
        return rebuild ( func, w, rank = nr, ks );
    }
    bool rebuild ( CCArrRef<Vector2d> & func, CCArrRef<bool> & w )
    {
        return rebuild ( func, w, rank, ks );
    }
};
Массив w позволяет исключать некоторые точки указав значение false.

Класс HarmAppr1 делает аппроксимацию периодических функций минимизируя 1-норму: 
class HarmAppr1 : public HarmAppr
{
    nat rank;
public:
    HarmAppr1 ( CCArrRef<Vector2d> & func, nat nr, nat k = 1 );
};
Ниже приведено сравнение методов HarmAppr1 и HarmAppr2:


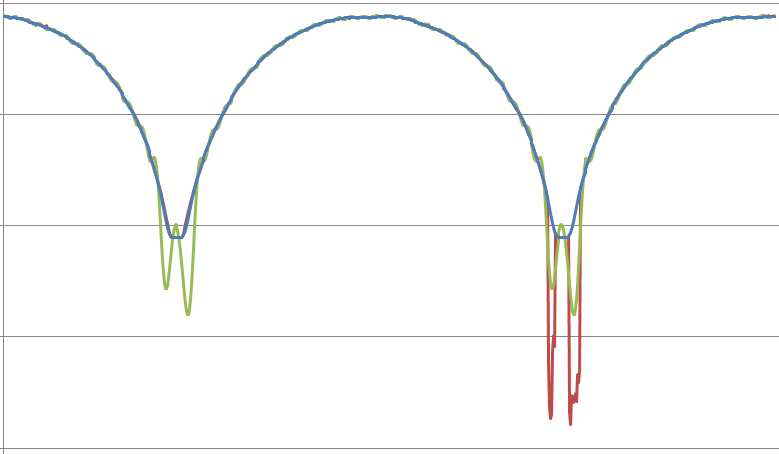Здесь красный цвет это исходные данные ( имеются выбросы ). Зелёный цвет - метод наименьших квадратов. Синий цвет - минимум 1-нормы ( выбросы игнорированы ).

Описание класса HMatrix находится здесь
Описание шаблонов классов CArrRef, ArrRef и DynArray находится здесь.

Исходники находятся в approx.cpp

Наверх